Ionization Energy of Hydrogen - Experiment vs. Theory

 x

from: Hydrogen's_Atomic_Emission_Spectrum

This paper explains one of the typical ways to extrapolate the ionization energy from hydrogen line measurements. 

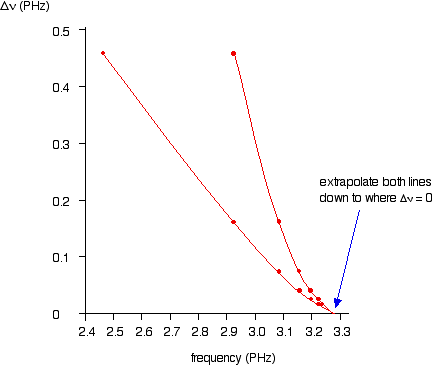
Consequently, if the increase in frequency is plotted against the actual frequency, the curve can be extrapolated to the point at which the increase becomes zero, the frequency of the series limit.

This extrapolation is required to be able to extract the frequency for the fully ionized $n={\infty}$ case for the ionization energy.  This is where the electron is pushed from the $n=1$ energy state (ground state or fundamental state) of hydrogen to the $n={\infty}$ (free state) and when the electron returns to the $n=1$ state, it gives off a photon of the frequency equal to the ionization energy (or frequency). 

Going back to the original equation for the energy of the electron (derived from the full two body proton-electron hydrogen atom Schrödinger equation):

$$E_{n}={-m_re^4\over8ce_0^2h^2n^2}$$

And, using $E=hf$, the ionization energy of hydrogen is:

$$E_{ionization}=E_0=E_{n=\infty\rightarrow1}=E_{n=\infty}-E_{n=1}={m_re^4\over8ce_0^2h^2}$$

Note the reduced mass term, $m_r$.  Here is where a potential misapplication of this equation can happen in concert with experimental data that can lead to possible misinterpretations of theory or experiment:

1. Step 1, since $m_r\equiv{m_pm_e\over m_p+m_e}$ and ${m_pm_e\over m_p+m_e}\approx m_e$, let $m_r=m_e$ <~~~reduced mass approximation
2. Since $m_r\approx m_e$, just assume the equation is valid for the electron, reducing the two body problem into a one body problem.  
3. Assume a quantum number/function, do experiment, and get excited how closely data matches theory!

Let's analyze the results of this experiment using the actual complete reduced mass term and compare it to using the reduced mass approximation:

From the linked experiment, the experimentally numerically/graphically extrapolated hydrogen ionization frequency is $3.28\times10^{15}Hertz$.  From this, the ionization energy can be calculated using:

$$E=hf$$

$E=h\times3.28\times10^{15}Hertz =$ 13.564990eV     <~~~ Experimental data

$E_{ionization}(m_r)={m_re^4\over8ce_0^2h^2}=$ 13.598287eV <~~~ Using reduced mass matches data better!!!

$E_{ionization}(m_e)={m_ee^4\over8ce_0^2h^2}=$ 13.605693eV <~~~ Using electron mass theory does not match data as well

Note using the reduced mass is a better match to the experimental data for the results of this one experiment.  Due to possible experimental error and the huge implications of this, it would be wise to check more than one experiment, however, I am confident all experiments of this type the data of the experiment will match the theory more closely if reduced mass is used rather than the electron mass. (I will check more and get back to ya if I find otherwise and retract this)

The purpose of this post's investigation is to determine if there is any experimental data to support our viewpoint about properly using the equations from theory, and first indications are there is support for our view.  Specifically, the handling of the proton to electron mass ratio and all the theoretical work around an atomic viewpoint of the proton and electron that is just slightly different than mainstream.  Actually, it may simply be turning into an interpretation question.  And, if correct, an approach that gives us all the masses and constants of physics via numerical algorithm.  This is the reason for pushing forward - to see if the algorithm is true (TOP-PCG2).  Also, this is favorable info for all the proton radius, mass ratio, and magnetic moment work.  Nothing conclusive, yet it is favorable.

While this changes little about mainstream science efforts and experiments, it should, perhaps, start opening minds to the idea that maybe, just maybe, something was missed, or passed over, or covered up, or just plain hidden.  The implications are great to science and humanity.

Forgot to mention, the other thing that may possibly come out of this, what I promised, a while back, a calculation - an equation for things such as muon mass, tau mass, these are likely, or the Higgs, or something, is in this error term (mixed in with the quantum number factor):
 $m_{err} = m_e-m_r$

 $m_{err} = m_e-{m_pm_e\over m_p+m_e}$

 $m_{err} = m_e{m_p+m_e\over m_p+m_e}-{m_pm_e\over m_p+m_e}$

 $m_{err} = {m_e^2\over m_p+m_e}$
that, combined with $\left({1\over l^2}+{1\over n^2}\right)$ might give some interesting masses and energies to find with this "goggle/viewpoint" of the mainstream, perhaps explaining some of the confusion on particle zoo follies over the years.  There are other terms for the quantum numbers in the parenthesis if things such as spin are considered in more detail which have been experimentally played with - key thing is it is all playing around unless there is a clear theoretical and experimental verification plan, and that's what all these years of hammering on the collider have been, looking at more and more advanced terms for the things in parenthesis while missing a blaring 4-5 decimal point error (1 in 2000? approx?) (and swept all errors, theoretical and measurement or otherwise, into a 4% proton radius error, and very, very likely, the same 4% error in the proton magnetic moment, and this overall 1/1836 or so error with this reduced mass assumption blunder, in all other constants, coefficients, and masses...)

The Surfer, OM-IV

Ω