Golden Ratio ($\varphi$) Fractally embedded in Nature - Platonic Solids

From wikipedia page on Platonic solid:

https://en.wikipedia.org/wiki/Platonic_solid

Cartesian coordinates[edit]

For Platonic solids centered at the origin, simple Cartesian coordinates are given below. The Greek letter φ is used to represent the golden ratio .

Cartesian coordinates

Figure	Tetrahedron		Octahedron	Cube	Icosahedron		Dodecahedron
Vertices	4		6 (2×3)	8	12 (4×3)		20 (8+4×3)
Orientation set	1	2			1	2	1	2
Coordinates	(1,1,1) (1,−1,−1) (−1,1,−1) (−1,−1,1)	(-1,-1,-1) (-1,1,1) (1,-1,1) (1,1,-1)	(±1, 0, 0) (0, ±1, 0) (0, 0, ±1)	(±1, ±1, ±1)	(0, ±1, ±φ) (±1, ±φ, 0) (±φ, 0, ±1)	(0, ±φ, ±1) (±φ, ±1, 0) (±1, 0, ±φ)	(±1, ±1, ±1) (0, ±1/φ, ±φ) (±1/φ, ±φ, 0) (±φ, 0, ±1/φ)	(±1, ±1, ±1) (0, ±φ, ±1/φ) (±φ, ±1/φ, 0) (±1/φ, 0, ±φ)
Image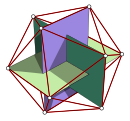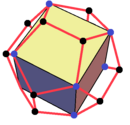

Note significantly $\varphi$,  the golden ratio .,  is all over the Platonic solids.

Considering that $\varphi$, the Golden ratio has been shown by many to be fractally embedded in all of Nature, Dan Winter's work is significanlty taking off where the ancients left off and giving meaning to:

https://en.wikipedia.org/wiki/Carved_Stone_Balls

...and more.
https://en.wikipedia.org/wiki/Toroidal_polyhedron <-- interesting as well!
https://en.wikipedia.org/wiki/Spherical_polyhedron

WHERE IS PEZ THE DUCK?   ~~~~~~~~~~~~~~~~~~~~~~~~~~~~>>>>>>>>>>>>>
Search for PEZ in this blog and bring him up the chain of posts to meet Bozon T. and his other Duck Family members!!!

PEZ

The Silver Surfer, OM-IV

Seinfled "The PEZ"

Ω