Sword of Science - SoS
Let's examine the expression for the electron mass and go through the exercise of how to put numbers to the equations and compare the results to CODATA measurements and previous mainstream theoretical predictions and analysis.
$$m_e={1 \over 2\alpha}\phi_e m_\ell$$
$m_e=$ mass of the electron
$m_\ell=$ Planck mass
$\phi_e={\eta_e\over R_e}=$ electron Holographic ratio
$\eta_e=$ Surface entropy
$R_e=$ Volume entropy
$\alpha=$ fine-structure constant
The subscript "e", for electron, is to emphasize that the $\eta_e$ and $R_e$ are to be calculated for the electron, using the confined electron's Bohr hydrogen radius atomic volume and the surface area to calculate $\eta$ and $R$.
Let's do $\eta$, the surface entropy first:
$$\eta=\eta_e$$
$$\eta_e={A_{e-surface}\over A_{eq}}$$
$$A_{e-surface}=4\pi {a_{0}}^2$$
$$A_{eq-PSU}=\pi {r_{\ell}}^2$$
$a_0=$ Bohr hydrogen radius - distance electron is away from proton center
$r_{\ell}$ is the Planck radius of the PSU
$r_{\ell}={\ell\over 2}$
$\ell=$ Planck length
$r_{\ell}={\ell\over 2}$
$\ell=$ Planck length
$A_{e-surface}$ is the surface area of a sphere of radius $a_0$, the Bohr radius.
$A_{eq-PSU}$ is the equatorial cross-sectional area of the Planck Spherical Unit (PSU).
$$\eta=\eta_e={4\pi {a_{0}}^2\over \pi {r_{\ell}}^2}$$
$R_e$, the volume entropy is next:
$$R_e={V_e\over V_{PSU}}$$
$$R_e={{4\over3}\pi a_0^3\over {4\over3}\pi r_{\ell}^3}={a_0^3\over r_{\ell}^3}$$
And finally:
$$\phi_e={\eta_e\over R_e}$$
$$\phi_e={4r_{\ell}\over a_0}$$
$$m_e={{1\over2\alpha}\phi_em_{\ell}}$$
Google link for m_e - mass of electron
CODATA Link to M_e electron mass
Check!!! Another success of Haramein's holographic approach.
Some further simplifications/reductions:
$$m_e={{1\over2\alpha}{4r_{\ell}\over a_0}m_{\ell}}$$
$$\eta=\eta_e={4\pi {a_{0}}^2\over \pi {r_{\ell}}^2}$$
$R_e$, the volume entropy is next:
$$R_e={V_e\over V_{PSU}}$$
$$R_e={{4\over3}\pi a_0^3\over {4\over3}\pi r_{\ell}^3}={a_0^3\over r_{\ell}^3}$$
And finally:
$$\phi_e={\eta_e\over R_e}$$
$$\phi_e={4r_{\ell}\over a_0}$$
$$m_e={{1\over2\alpha}\phi_em_{\ell}}$$
$$m_e={{1\over2\alpha}{4r_{\ell}\over a_0}m_{\ell}}$$
Google calculator expression:
https://www.google.com/search?q=hbar%3D&oq=hbar%3D&aqs=chrome..69i57.3102j0j8&sourceid=chrome&ie=UTF-8#q=(1%2F(2*(fine-structure+constant))*4*(sqrt(hbar*G%2Fc%5E3)%2F2%2F(hbar%2F(m_e*c*(fine-structure+constant)))*sqrt(hbar*c%2FG)%3D
Google calculator expression:
https://www.google.com/search?q=hbar%3D&oq=hbar%3D&aqs=chrome..69i57.3102j0j8&sourceid=chrome&ie=UTF-8#q=(1%2F(2*(fine-structure+constant))*4*(sqrt(hbar*G%2Fc%5E3)%2F2%2F(hbar%2F(m_e*c*(fine-structure+constant)))*sqrt(hbar*c%2FG)%3D
Google link for m_e - mass of electron
electron mass =
9.10938356 × 10-31 kilograms
CODATA Link to M_e electron mass
electron mass 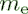 | |
| Value | 9.109 383 56 x 10-31 kg |
| Standard uncertainty | 0.000 000 11 x 10-31 kg |
| Relative standard uncertainty | 1.2 x 10-8 |
| Concise form | 9.109 383 56(11) x 10-31 kg |
Check!!! Another success of Haramein's holographic approach.
Some further simplifications/reductions:
$$m_e={{1\over2\alpha}{4r_{\ell}\over a_0}m_{\ell}}$$
$$m_e={\ell m_{\ell}\over\alpha a_0}$$
$$\ell=\sqrt{\hbar G \over c^3}$$
https://en.wikipedia.org/wiki/Bohr_radius
$$m_{\ell}=\sqrt{\hbar c\over G}$$
$${\ell}m_{\ell}={\hbar\over c}$$
$${\ell}m_{\ell}={\hbar\over c}$$
$$m_e={\hbar\over c\alpha a_0}$$
$$a_0={\hbar\over m_ec\alpha}$$
The Surfer, OM-IV


No comments:
Post a Comment
Watch the water = Lake 👩 🌊🦆