Another Equation for Proton to Electron Mass Ratio???

Using Haramein's The Electron and the Holographic Mass Solution:

$$\mu={m_p\over m_e}={2\phi m_{\ell}\over {\phi_em_{\ell}/2\alpha}}=4\alpha{\phi\over\phi_e}=4\alpha{a_0\over r_p}=1836.15267...$$
Compare to:
$$\mu={\alpha^2\over{\pi r_pR_{\infty}}}=1836.15267...$$
$\mu=$ proton to electron  mass ratio
$m_p=$ mass of proton

$m_e=$ mass of electron
$\phi={\eta\over R}$ Holographic ratio for proton

$\phi_e={\eta_e\over R_e}$ Holographic ratio for electron
$m_{\ell}=$ Planck mass
$a_0=$ Bohr radius
$r_p=$ proton radius (muonic hydrogen proton radius)
$R_{\infty}=$ Rydberg constant

Google calculator link and results snapshot:

https://www.google.com/search?q=4*(fine-structure+constant)*hbar%2F(m_e*c*(fine-structure+constant))%2F(4*hbar%2Fc%2Fm_p)%3D&rlz=1C1CHWA_enUS566US567&oq=4*(fine-structure+constant)*hbar%2F(m_e*c*(fine-structure+constant))%2F(4*hbar%2Fc%2Fm_p)%3D&aqs=chrome..69i57.12066j0j8&sourceid=chrome&ie=UTF-8

((4 * fine-structure constant * hbar) / (m_e * c * fine-structure constant)) / (((4 * hbar) / c) / m_p) =

1 836.15267

CODATA value for proton-electron mass ratio:
http://physics.nist.gov/cgi-bin/cuu/Value?mpsme

proton-electron mass ratio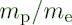
Value	1836.152 673 89
Standard uncertainty	0.000 000 17
Relative standard uncertainty	9.5 x 10-11
Concise form	1836.152 673 89(17)

There remain a few issues to be ironed out as Haramein's paper, The Electron and the Holographic Mass Solution, reports the proton to electron mass ratio as:
$$\mu={m_p\over m_e}={2\phi m_{\ell}\over {\phi_em_{\ell}/2\alpha}}=4\alpha{\phi\over\phi_e}=1836.942579077855...$$

So, the work continues to understand this difference...

This result, the 1836.94259077855... above, is calculated using the CODATA value for $\alpha$, the 2013 muonic hydrogen charge radius in the $phi$ calculation, and $phi_e=6.108458512E-25$ .  See Google Drive Excel File for calculations.

More in upcoming post: Another Equation for Proton to Electron Mass Ratio!!! #2

The Surfer, OM-IV

Ω