Maxwell's Equations #1

An interesting fact about Maxwell's Equations is (from wikilink):

"The direct space–time formulations make manifest that the Maxwell equations are relativistically invariant (in fact studying the hidden symmetry of the vector calculus formulation was a major source of inspiration for relativity theory). "

That means they already had relativity built into them EVEN before 1905:
 http://en.wikipedia.org/wiki/Albert_Einstein#1905_.E2.80.93_Annus_Mirabilis_papers

We are going to examine how Maxwell's Equations are used to investigate certain phenomena, like, look at the boundary conditions and initial conditions and formulations of problems to:

1. Understand Maxwell's field equations and their significance
2. See how some simple cases are used in technology
3. Look at solutions wholly as the Electric Universe people have done
4. What is required for a ToE? (Theory of Everything)

The Electric Universe Theory (EUT), which I find very complimentary to the Unified Physics of Nassim Haramein (Haramein Unified THeory - HUT) et al, however, my investigation is ongoing, and being that I am looking for a GUT or HUT, and it is now very clear going down these paths (EU and HUT) in our continuing investigation is the way to go.

Maxwell's Equations are the theory behind what I do to make a living - designing mixed signal analog digital circuits that work in real modern advanced systems - the stuff that makes your cell phone base stations easily programmable via software to create a new modulation/coding/whatever scheme (3G, 4G, NextGen like idea).  Software radio like stuff, which can be done with very high speed low noise interpolating D-A converters. The stuff was so advanced, it was the first stuff we had to get approval to send oversees...

So, that said, I am going to revisit Maxwell's Equations and see what others have done in the last century, focusing on modern developments in light of insight into the unified physics approach.

A quick preview example:

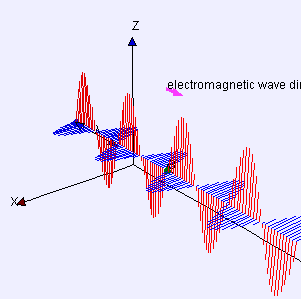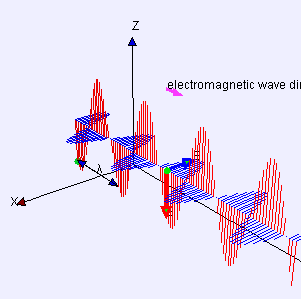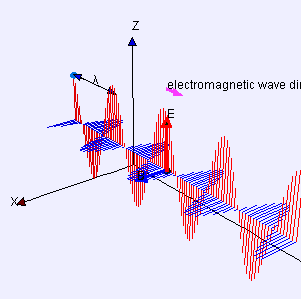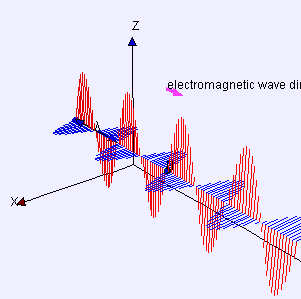
Gauss's law for magnetism: magnetic field lines never begin nor end but form loops or extend to infinity as shown here with the magnetic field due to a ring of current.

I want to look into, for example, a magnetic monopole, as some recent researchers have done:

Ref. 2

A condensate of cold atoms can be a model for a magnetic monopole, in which the magnetic field jots out of an isolated pole — except in one direction where there is no field.

Anyway, there is QUITE a difference between these two images and something implied by magnetic monopoles that we need to look into...

(MRGMVIEW Don't Starve - a fun diversion)

More later,

The Surfer, OM-IV

Ω