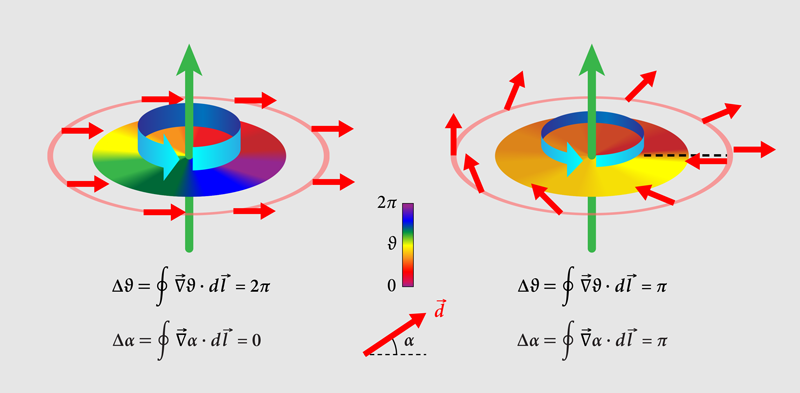
Vortex-quantization in a superfluid, circulation is quantized:
$$\oint_C\mathbf{v}\cdot d\mathbf{l}={2\pi\hbar\over m}n$$
$\mathbf{v}=$ velocity
$\mathbf{l}=$ path length, $d\mathbf{l}=rd\theta$, for dot product
$\hbar={h\over{2\pi}}$ = Reduced Planck's constant, and $h$, Planck's constant
$m=$ mass
$n=$ integer, quantized
for uniform circular motion, constant velocity:
$\oint_Cd\mathbf{l}={\int_0}^{2\pi}rd\theta=2\pi r$, circumference of circle
$$\oint_C\mathbf{v}\cdot d\mathbf{l}={\mathbf{v}2\pi r}$$
$${\mathbf{v}2\pi r}={2\pi\hbar\over m}n$$
$${m r}={2\pi\hbar\over {\mathbf{v}2\pi}}n$$
$${m r}={\hbar\over {\mathbf{v}}}n$$
$${m r}={nh\over {2\pi\mathbf{v}}}$$
For a proton that is a vibration in the superfluid vacuum aether, the phase velocity of circulation is the speed of light, $c$:
$$\therefore{m r}={nh\over {2\pi c}}$$
the proton being the $n=4$ case:
$$\therefore{m r}={2h\over {\pi c}}$$
which is the same equation derived for the proton using the quantized angular momentum approach and Haramein's team's geometrical information theory holofractographic approach.
This is implying that the vacuum is a superfluid.
Still need to derive why the proton mass is what it is... and why the proton is the $n=4$ case.