Metallic mean

Gold, silver, and bronze ratios within their respective rectangles.

The metallic mean (also metallic ratio, metallic constant, or noble mean^[1]) of a natural number n is a positive real number, denoted here ${\displaystyle S_n,}$ that satisfies the following equivalent characterizations:

• the unique positive real number ${\displaystyle x}$ such that $x=n+\frac{1}{x}$
• the positive root of the quadratic equation ${\displaystyle x^2-nx-1=0}$
• the number $\frac{n+\sqrt{n^2+4}}{2}=\frac{2}{\sqrt{n^2+4}-n}$
• the number whose expression as a continued fraction is

  ${\displaystyle [n;n,n,n,n,\dots ]=n+\frac{1}{n+\frac{1}{n+\frac{1}{n+\frac{1}{n+\ddots }}}}}$

Metallic means are (successive) derivations of the golden (${\displaystyle n=1}$) and silver ratios (${\displaystyle n=2}$), and share some of their interesting properties. The term "bronze ratio" (${\displaystyle n=3}$) (Cf. Golden Age and Olympic Medals) and even metals such as copper (${\displaystyle n=4}$) and nickel (${\displaystyle n=5}$) are occasionally found in the literature.^[2][3][a]

In terms of algebraic number theory, the metallic means are exactly the real quadratic integers that are greater than ${\displaystyle 1}$ and have ${\displaystyle -1}$ as their norm.

The defining equation ${\displaystyle x^2-nx-1=0}$ of the nth metallic mean is the characteristic equation of a linear recurrence relation of the form ${\displaystyle x_k=n{x}_{k-1}+x_{k-2}.}$ It follows that, given such a recurrence the solution can be expressed as

${\displaystyle x_k=a{S}_n^k+b{\left(\frac{-1}{S_n}\right)}^k,}$

where ${\displaystyle S_n}$ is the nth metallic mean, and a and b are constants depending only on ${\displaystyle x_0}$ and ${\displaystyle x_1.}$ Since the inverse of a metallic mean is less than 1, this formula implies that the quotient of two consecutive elements of such a sequence tends to the metallic mean, when k tends to the infinity.

For example, if ${\displaystyle n=1,}$ ${\displaystyle S_n}$ is the golden ratio. If ${\displaystyle x_0=0}$ and ${\displaystyle x_1=1,}$ the sequence is the Fibonacci sequence, and the above formula is Binet's formula. If ${\displaystyle n=1,x_0=2,x_1=1}$ one has the Lucas numbers. If ${\displaystyle n=2,}$ the metallic mean is called the silver ratio, and the elements of the sequence starting with ${\displaystyle x_0=0}$ and ${\displaystyle x_1=1}$ are called the Pell numbers.

Geometry

If one removes n largest possible squares from a rectangle with ratio length/width equal to the nth metallic mean, one gets a rectangle with the same ratio length/width (in the figures, n is the number of dotted lines).

Golden ratio within the pentagram (φ = red/ green = green/blue = blue/purple) and silver ratio within the octagon.

The defining equation $x=n+\frac{1}{x}$ of the nth metallic mean induces the following geometrical interpretation.

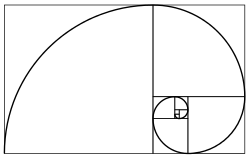
Consider a rectangle such that the ratio of its length L to its width W is the nth metallic ratio. If one remove from this rectangle n squares of side length W, one gets a rectangle similar to the original rectangle; that is, a rectangle with the same ratio of the length to the width (see figures).

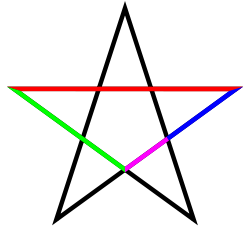
Some metallic means appear as segments in the figure formed by a regular polygon and its diagonals. This is in particular the case for the golden ratio and the pentagon, and for the silver ratio and the octagon; see figures.

Powers

Denoting by ${\displaystyle S_m}$ the metallic mean of m one has

${\displaystyle S_m^n=K_n{S}_m+K_{n-1},}$

where the numbers ${\displaystyle K_n}$ are defined recursively by the initial conditions K₀ = 0 and K₁ = 1, and the recurrence relation

${\displaystyle K_n=m{K}_{n-1}+K_{n-2}.}$

Proof: The equality is immediately true for ${\displaystyle n=1.}$ The recurrence relation implies ${\displaystyle K_2=m,}$ which makes the equality true for ${\displaystyle k=2.}$ Supposing the equality true up to ${\displaystyle n-1,}$ one has

End of the proof.

One has also ^{[citation needed]}

${\displaystyle K_n=\frac{S_m^{n+1}-(m-S_m{)}^{n+1}}{\sqrt{m^2+4}}.}$

The odd powers of a metallic mean are themselves metallic means. More precisely, if n is an odd natural number, then ${\displaystyle S_m^n=S_{M_n},}$ where ${\displaystyle M_n}$ is defined by the recurrence relation ${\displaystyle M_n=m{M}_{n-1}+M_{n-2}}$ and the initial conditions ${\displaystyle M_0=2}$ and ${\displaystyle M_1=m.}$

Proof: Let ${\displaystyle a=S_m}$ and ${\displaystyle b=-1/S_m.}$ The definition of metallic means implies that ${\displaystyle a+b=m}$ and ${\displaystyle ab=-1.}$ Let ${\displaystyle M_n=a^n+b^n.}$ Since ${\displaystyle a^n{b}^n=(ab{)}^n=-1}$ if n is odd, the power ${\displaystyle a^n}$ is a root of ${\displaystyle x^2-M_n-1=0.}$ So, it remains to prove that ${\displaystyle M_n}$ is an integer that satisfies the given recurrence relation. This results from the identity

This completes the proof, given that the initial values are easy to verify.

In particular, one has

and, in general,^{[citation needed]}

${\displaystyle S_m^{2n+1}=S_M,}$

where

${\displaystyle M=\sum _{k=0}^n\frac{2n+1}{2k+1}(\genfrac{}{}{0ex}{}{n+k}{2k})m^{2k+1}.}$

For even powers, things are more complicated. If n is a positive even integer then^{[citation needed]}

${\displaystyle S_m^n-\lfloor S_m^n\rfloor =1-S_m^{-n}.}$

Additionally,^{[citation needed]}

${\displaystyle \frac{1}{S_m^4-\lfloor S_m^4\rfloor }+\lfloor S_m^4-1\rfloor =S_{\left(m^4+4m^2+1\right)}}$

${\displaystyle \frac{1}{S_m^6-\lfloor S_m^6\rfloor }+\lfloor S_m^6-1\rfloor =S_{\left(m^6+6m^4+9m^2+1\right)}.}$

For the square of a metallic ratio we have:${\displaystyle S_m^2=[m\sqrt{m^2+4}+(m+2)]/2=(p+\sqrt{p^2+4})/2}$

where ${\displaystyle p=m\sqrt{m^2+4}}$ lies strictly between ${\displaystyle m^2+1}$ and ${\displaystyle m^2+2}$. Therefore

Generalization

One may define the metallic mean ${\displaystyle S_{-n}}$ of a negative integer −n as the positive solution of the equation ${\displaystyle x^2-(-n)x-1.}$ The metallic mean of −n is the multiplicative inverse of the metallic mean of n:

${\displaystyle S_{-n}=\frac{1}{S_n}.}$

Another generalization consists of changing the defining equation from ${\displaystyle x^2-nx-1=0}$ to ${\displaystyle x^2-nx-c=0}$. If

${\displaystyle R=\frac{n\pm \sqrt{n^2+4c}}{2},}$

is any root of the equation, one has

${\displaystyle R-n=\frac{c}{R}.}$

The silver mean of m is also given by the integral^[4]

${\displaystyle S_m={\int }_0^m\left(\frac{x}{2\sqrt{x^2+4}}+\frac{m+2}{2m}\right)dx.}$

Another form of the metallic mean is^[4]

${\displaystyle \frac{n+\sqrt{n^2+4}}{2}=e^{\mathrm{a}\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{h}(\mathrm{n}/2)}.}$

Relation to half-angle cotangent

A tangent half-angle formula gives$${\displaystyle \cot \theta =\frac{{\cot }^2\frac{\theta }{2}-1}{2\cot \frac{\theta }{2}}}$$which can be rewritten as$${\displaystyle {\cot }^2\frac{\theta }{2}-(2\cot \theta )\cot \frac{\theta }{2}-1=0.}$$That is, for the positive value of $\cot \frac{\theta }{2}$, the metallic mean$${\displaystyle S_{2\cot \theta }=\cot \frac{\theta }{2},}$$which is especially meaningful when $2\cot \theta$ is a positive integer, as it is with some Pythagorean triangles.

Relation to Pythagorean triples

Metallic Ratios in Primitive Pythagorean Triangles

For a primitive Pythagorean triple, a² + b² = c², with positive integers a < b < c that are relatively prime, if the difference between the hypotenuse c and longer leg b is 1, 2 or 8 then the Pythagorean triangle exhibits a metallic mean. Specifically, the cotangent of one quarter of the smaller acute angle of the Pythagorean triangle is a metallic mean.^[5]

More precisely, for a primitive Pythagorean triple (a, b, c) with a < b < c, the smaller acute angle α satisfies$${\displaystyle \tan \frac{\alpha }{2}=\frac{c-b}{a}.}$$When c − b ∈ {1, 2, 8}, we will always get that$${\displaystyle n=2\cot \frac{\alpha }{2}=\frac{2a}{c-b}}$$is an integer and that$${\displaystyle \cot \frac{\alpha }{4}=S_n,}$$the n-th metallic mean.

The reverse direction also works. For n ≥ 5, the primitive Pythagorean triple that gives the n-th metallic mean is given by (n, n²/4 − 1, n²/4 + 1) if n is a multiple of 4, is given by (n/2, (n² − 4)/8, (n² + 4)/8) if n is even but not a multiple of 4, and is given by (4n, n² − 4, n² + 4) if n is odd. For example, the primitive Pythagorean triple (20, 21, 29) gives the 5th metallic mean; (3, 4, 5) gives the 6th metallic mean; (28, 45, 53) gives the 7th metallic mean; (8, 15, 17) gives the 8th metallic mean; and so on.

Numerical values

First metallic means[6][7]
n	Ratio	Value	Name
${\displaystyle n}$	${\displaystyle \frac{n+\sqrt{4+n^2}}{2}}$
0	${\displaystyle \frac{0+\sqrt{4}}{2}=1}$	1
1	${\displaystyle \frac{1+\sqrt{5}}{2}}$	1.618033988...[8]	Golden
2	${\displaystyle \frac{2+\sqrt{8}}{2}=1+\sqrt{2}}$	2.414213562...[9]	Silver
3	${\displaystyle \frac{3+\sqrt{13}}{2}}$	3.302775637...[10]	Bronze[11]
4	${\displaystyle \frac{4+\sqrt{20}}{2}=2+\sqrt{5}}$	4.236067977...[12]	Copper[11][a]
5	${\displaystyle \frac{5+\sqrt{29}}{2}}$	5.192582403...[13]	Nickel[11][a]
6	${\displaystyle \frac{6+\sqrt{40}}{2}=3+\sqrt{10}}$	6.162277660...[14]
7	${\displaystyle \frac{7+\sqrt{53}}{2}}$	7.140054944...[15]
8	${\displaystyle \frac{8+\sqrt{68}}{2}=4+\sqrt{17}}$	8.123105625...[16]
9	${\displaystyle \frac{9+\sqrt{85}}{2}}$	9.109772228...[17]
10	${\displaystyle \frac{10+\sqrt{104}}{2}=5+\sqrt{26}}$	10.099019513...[18]

See also

• Constant
• Mean
• Ratio
• Plastic ratio