Exploring Julia Sets: The Fractal Companions to the Mandelbrot Set

Exploring Julia Sets: The Fractal Companions to the Mandelbrot Set

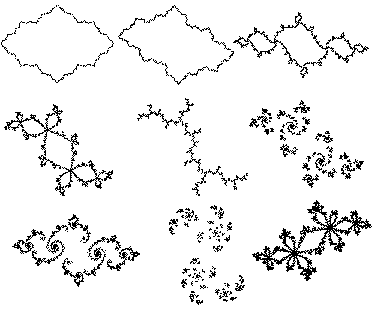
Julia sets are a family of fractals in the complex plane, named after the French mathematician Gaston Julia who studied them in the early 20th century. They are intimately connected to the Mandelbrot set, which acts as a "map" or index for all possible Julia sets. While the Mandelbrot set is a single fractal showing which values of a complex parameter c produce connected Julia sets, each Julia set itself is generated for a fixed c and explores the behavior of iterated quadratic functions. These sets are renowned for their infinite complexity, with boundaries that reveal self-similar patterns, spirals, and intricate details upon zooming—much like the Mandelbrot but varying wildly in shape from connected "fatou dust" to disconnected "cantor dust" depending on c.

Mathematically, a Julia set J(c) for a complex number c is the boundary between points z in the complex plane that remain bounded under iteration z_{n+1} = z_n² + c (starting from z_0 = z) and those that escape to infinity. Points inside the set (the filled Julia set) stay finite; the boundary is the actual fractal. The escape criterion is typically |z_n| > 2 after a maximum number of iterations (e.g., 100-1000), with colors assigned based on escape speed for visualization. For c inside the Mandelbrot set, J(c) is connected; outside, it's disconnected into dust-like points.

Julia sets exemplify dynamical systems and chaos theory: Small changes in c produce vastly different fractals, from bulbous shapes to dendritic trees. They also relate to the Fatou-Julia theorem, which classifies periodic points into attracting cycles (Fatou domains) or repelling (Julia set).

Let's dive into specific examples to explore their diversity.

Classic Connected Julia Set (c = -0.8 + 0.156i)

This value produces a connected, dragon-like shape with swirling tendrils, showcasing the set's chaotic boundary where points barely escape or remain trapped. It's a prime example of how Julia sets can mimic biological forms through iteration.

mcgoodwin.net

Julia Sets

Dendritic Julia Set (c = 0.285 + 0.01i)

Here, the set forms tree-like dendrites with branching patterns, illustrating how slight imaginary components create asymmetric, organic structures. This one highlights the fractal's infinite recursion—zooming into branches reveals smaller copies.

researchgate.net

An example of a fractal known as the Julia set [47] for a ...

Disconnected Julia Dust (c = 0.8)

For c outside the Mandelbrot set, the Julia set disintegrates into Cantor dust—disconnected points scattering like fractal powder. This shows the transition from connectedness to total fragmentation.

gauss.math.yale.edu

Fractal Geometry

Exploring Julia sets reveals the beauty of complex dynamics: A simple equation z² + c yields universes of form. In the Super Golden TOE, similar iterations could model aether cascades, where φ-scaled c values ensure stable, non-diverging "bounded" physics. For deeper dives, tools like Fractal Explorer or code in Python/Mathematica can generate custom sets—try c = -0.123 + 0.745i for the "Douady rabbit"!